Soru Sor sayfası kullanılarak Dörtgenler konusu altında Dörtgende Orta Tabanı Kullanarak Alan Bulma ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU


2.SORU
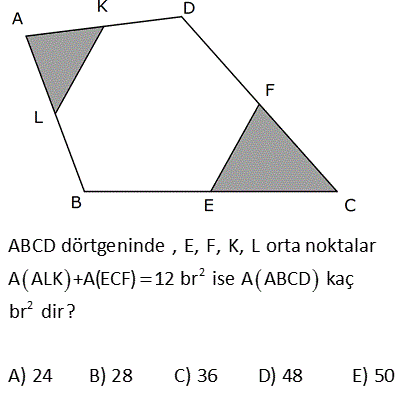
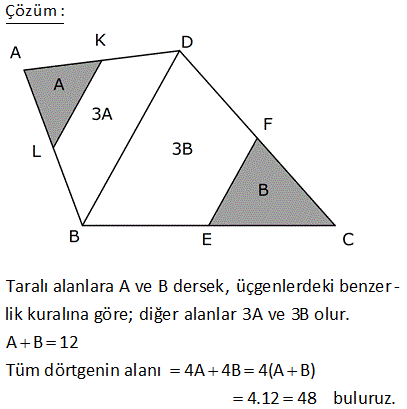
3.SORU
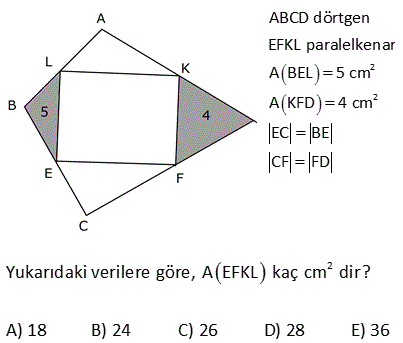
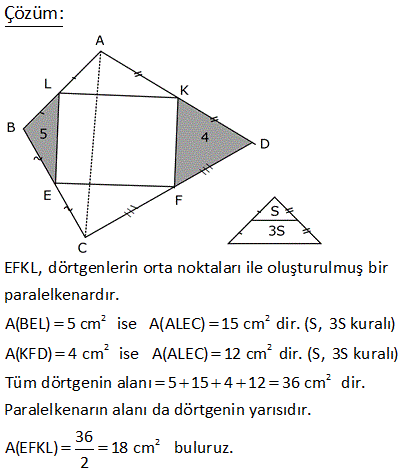
4.SORU
5.SORU
6.SORU
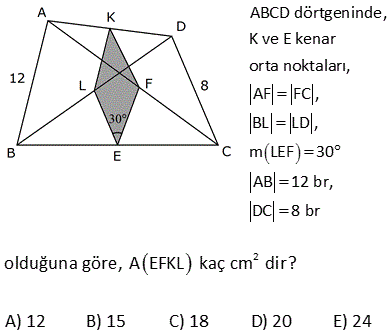
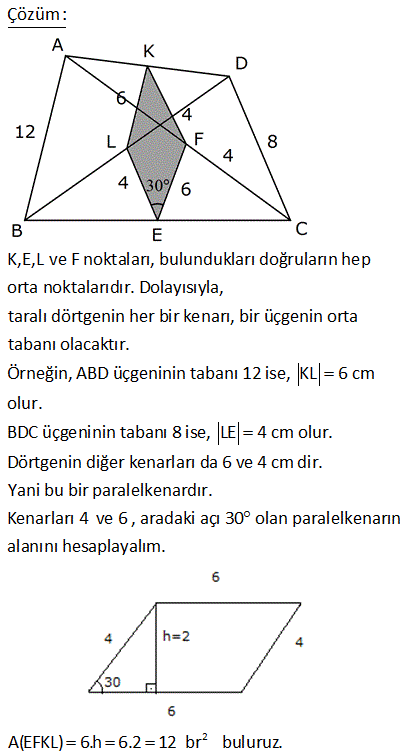
7.SORU


Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Çıkmış Sorular İçin Tıklayınız.
Abone olarak daha fazla sayıda soru sorabilirsiniz. Abone olmak için Tıklayın.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Not: Bu sitede yayınlanan çözümler, tamamen bu site için hazırlanmıştır. İzinsiz olarak yayınlanıp, çoğaltılması yasaktır.
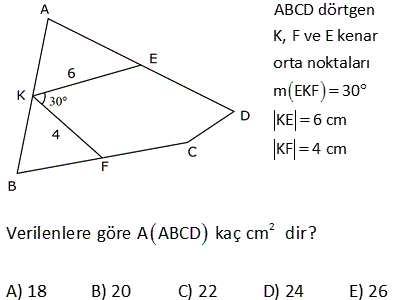
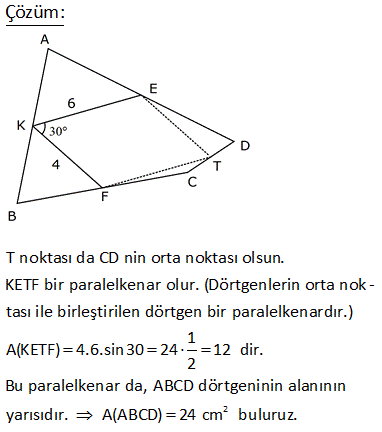
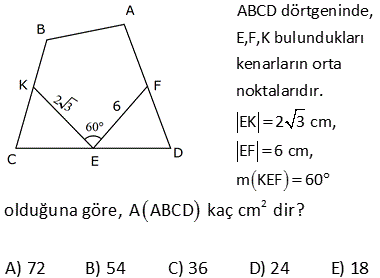
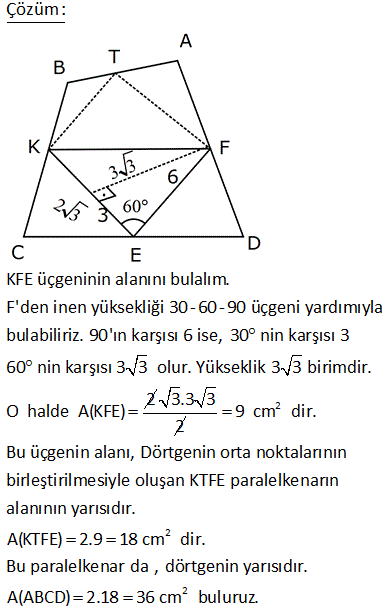
2 ABCD dörtgen, E, F ve G noktaları orta noktalar m EFG 120 , EF 4 3 cm, FG 4 cm Yukarıdaki verilere göre, A ABCD kaç cm dir? A) 24 B) 36 C) 48 D) 60 E) 72 1 EFG üçgeninin alanı 4 3 4 sin120 2 1 3 1 4 3 4 2 2 2 4 3 4 3 2 12 dir. EFGH paralelkenarının alanı, üçgeninin alanın 2 katıdır. Tüm dörtgenin alanı da EFGH paralelkenarının 2 katıdır. Buna göre; A(ABCD) 12.2.2 48 buluruz. 9 2 2 ABCD dörtgeninde , E, F, K, L orta noktalar A ALK +A(ECF) 12 br ise A ABCD kaç br dir? A) 24 B) 28 C) 36 D) 48 E) 50 Taralı alanlara A ve B dersek, üçgenlerdeki benzer – lik kuralına göre; diğer alanlar 3A ve 3B olur. A B 12 Tüm dörtgenin alanı 4A 4B 4(A B) 4. 12 48 buluruz. 12 2 2 ABCD dörtgen EFKL paralelkenar A BEL 5 cm A KFD 4 cm EC BE CF FD 2 Yukarıdaki verilere göre, A EFKL kaç cm dir? A) 18 B) 24 C) 26 D) 28 E) 36 2 2 2 2 EFKL, dörtgenlerin orta noktaları ile oluşturulmuş bir paralelkenardır. A(BEL) 5 cm ise A(ALEC) 15 cm dir. (S, 3S kuralı) A(KFD) 4 cm ise A(ALEC) 12 cm dir. (S, 3S kuralı) Tüm dörtgenin alanı 5 2 2 15 4 12 36 cm dir. Paralelkenarın alanı da dörtgenin yarısıdır. 36 A(EFKL) 18 cm buluruz. 2 20 ABCD dörtgen K, F ve E kenar orta noktaları m EKF 30 KE 6 cm KF 4 cm 2 Verilenlere göre A ABCD kaç cm dir? A) 18 B) 20 C) 22 D) 24 E) 26 T noktası da CD nin orta noktası olsun. KETF bir paralelkenar olur. (Dörtgenlerin orta nok – tası ile birleştirilen dörtgen bir paralelkenardır.) 1 A(KETF) 4.6.sin30 24 12 dir. 2 Bu paralelkenar da, ABCD d 2 örtgeninin alanının yarısıdır. A(ABCD) 24 cm buluruz. 25 ABCD dörtgeninde, E,F,K bulundukları kenarların orta noktalarıdır. EK 2 3 cm, EF 6 cm, m KEF 60 2 olduğuna göre, A ABCD kaç cm dir? A) 72 B) 54 C) 36 D) 24 E) 18 KFE üçgeninin alanını bulalım. F’den inen yüksekliği 30 – 60 – 90 üçgeni yardımıyla bulabiliriz. 90’ın karşısı 6 ise, 30 nin karşısı 3 60 nin karşısı 3 3 olur. Yükseklik 3 3 birimdir. 2 O halde A(KFE) 3.3 3 2 2 2 9 cm dir. Bu üçgenin alanı, Dörtgenin orta noktalarının birleştirilmesiyle oluşan KTFE paralelkenarın alanının yarısıdır. A(KTFE) 2.9 18 cm dir. Bu paralelkenar da , dörtgenin yarısıdır. A(ABCD) 2.18 2 36 cm buluruz. 47 ABCD dörtgeninde, K ve E kenar orta noktaları, AF FC , BL LD , m LEF 30 AB 12 br, DC 8 br 2 olduğuna göre, A EFKL kaç cm dir? A) 12 B) 15 C) 18 D) 20 E) 24 K,E,L ve F noktaları, bulundukları doğruların hep orta noktalarıdır. Dolayısıyla, taralı dörtgenin her bir kenarı, bir üçgenin orta tabanı olacaktır. Örneğin, ABD üçgeninin tabanı 12 ise, KL 6 cm olur. BDC üçgeninin tabanı 8 ise, LE 4 cm olur. Dörtgenin diğer kenarları da 6 ve 4 cm dir. Yani bu bir paralelkenardır. Kenarları 4 ve 6 , aradaki açı 30 olan paralelkenarın alanını hesaplayalım. 2 A(EFKL) 6. h6.212 br buluruz. 49 ABCD dörtgen m KEF 60 KE 4 cm EF 6 cm 2 Yukarıdaki şekilde E,F ve K kenar orta noktaları olduğuna göre, A ABCD kaç cm dir? A) 12 3 B) 16 3 C) 24 3 D) 32 3 E) 36 3 T noktası BC’nin orta noktası olsun. Bir dörtgende orta noktaların birleştirilmesiyle oluşan dörtgen bir paralelkenardır. Dolayısıyla KETF bir paralelkenardır. Sinüs alan formülünü kullanalım. A(KETF) KE . EF .sin60 4 2 3 .6 2 2 2 12 3 cm dir. ABCD dörtgeninin alanı da bu paralelkenarın alanı – nın 2 katıdır. A ABCD 2.12 3 24 3 cm buluruz. 59

