Nitelikli Sayı Problemi

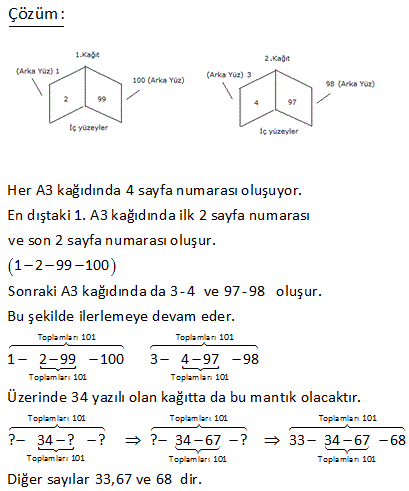
Tezgahta 60 gün bozulmadan duran incir, depoda 75 gün bozulmadan durabiliyor. Eşit miktarlarda iki kutu incirden biri tezgaha diğeri depoya aynı anda konuyor ve 10 gün sonra incir kutuları yer değiştiriliyor. Buna göre, erken bozulan incir toplam kaç gün dayanmıştır? A) 62 B) 63 C) 64 D) 65 E) 66 www.matematikkolay.net Çözüm: Tezgahta 10 gün duran incir, 10 1 Dayanma sınırının ‘sını harcamıştır. 60 6 5 Geriye ‘sı kalmıştır. Depoda ise bozulmadan 6 5 6 5 kalabileceği süre 1 6 75    2 75  25 125 62,5 gün 1 2 Toplam 10 62,5 72,5 gün dayanmıştır. Depoda 10 gün duran incir, 10 2 Dayanma sınırının ‘ini harcamıştır. 75 15 13 Geriye ‘i kalmıştır. Tezgahta ise bozulmadan 15 13 15 13 kalabileceği süre 1 1 60        5 60  4 52 gündür. 1 Toplam 10 52 62 gün dayanmıştır. Erken bozulan, 62 gün dayanmıştır.     171 Bir taş sanatçısı renkli taşları üst üste koyarak çiçek veya yıldız motifleri elde ediyor. Bu sanatçı her sırada • 25 tane olmak üzere 4 sıra taşla bir çiçek motifi • 30 tane olmak üzere 3 sıra taşlı bir yıldız motifi oluşturuyor. Bu sanatçı, toplam 1150 tane taş kullanarak 12 tane motif oluşturduğuna göre, oluşturduğu çiçek motifi sayısı kaçtır? Çıkmış Soru www.matematikkolay.net Çözüm: Bir çiçek motifi 25.4 100 taş ile yapılabiliyor. Bir yıldız motifi ise 30.3 90 taş ile yapılabiliyor. Çiçek motifi sayısı x olsun. Yıldız motifi sayısı 12 x olur. O halde toplam taş sayılarını e      şitleyen şöyle bir denklem kurabiliriz : x.100 12 x .90 1150 100x 1080 90x 1150 1080 10x 1150 10x 70 x 7 buluruz. Cevap: 7           174 25 tane A3 kağıdı şekildeki ikiye katlanarak elde edilen A4 kağıt sayfalarına 1,2,3,4,…,98,99,100 numaraları yazılıyor. Buna göre 34 numaralı A4 sayfasını bulunduğu A3 kağıdındaki diğer numaralar aşağıdakilerden hangisidir? A) 35-67-68 B) 33-66 -67 C) 35-66 -67 D) 32-68 -69 E) 33-67-68 www.matematikkolay.net Çözüm:   Her A3 kağıdında 4 sayfa numarası oluşuyor. En dıştaki 1. A3 kağıdında ilk 2 sayfa numarası ve son 2 sayfa numarası oluşur. 1 2 99 100 Sonraki A3 kağıdında da 3 – 4 ve 97 – 98 oluşur. Bu şekilde ilerlemeye    Toplamları 101 Toplamları 101 Toplamları 101 Toplamları 101 Toplamları 101 Toplamları 101 devam eder. 1 2 99 100 3 4 97 98 Üzerinde 34 yazılı olan kağıtta da bu mantık olacaktır. ? 34 ? ?          Toplamları 101 Toplamları 101 Toplamları 101 Toplamları 101 ? 34 67 ? 33 34 67 68 Diğer sayılar 33,67 ve 68 dir.         195 Bir şirkette, incelenmek üzere 144 adet dosya tüm çalışanlar arasında eşit olarak paylaştırılmıştır. Bahadır,payına düşen sayıda dosyayı inceledikten sonra izne ayrılmış, 4 çalışan ise işten ayrıldığı için hiç dosya incelememiştir.İzinde olmayan çalışanlar, işten ayrılan bu kişilerin dosyalarını da eşit olarak paylaşmış ve bu dosyalar ile başlangıçta kendi paylarına düşen dosyaları incelemiştir. Bahadır bir iş arkadaşınınincelediği dosya sayısının yarısı kadarını incelediğine göre, Bahadır’ın incelediği dosya sayısı kaçtır? www.matematikkolay.net Çözüm: Bu şirkette başlangıçta x çalışan olsun. 144 Her çalışana kadar dosya düşer. x 144 Bahadır kadar dosyayı bitirip; izine ayrılmış. x 4 çalışan da işten ayrılınca toplam çalışan sayısı x 5 olur. 4 kişini  144 n işi 4 tir ve bu iş diğer çalışanlara x ekstra dağıtılıcaktır. Buna göre (x 5) çalışandan her biri toplam 144 144 4 iş yapmıştır. x x.(x 5) Bu çalışanlar, Bahadır’ın iki katı iş yaptığına göre; 144 4 x        144 144 2 x.(x 5) x 144 4     x 144 .(x 5)   x 4 1 x 5 4 x 9 dur. x 5 144 Bahadır’ın dosya sayısı 16 dır. 9          19 Ege üst üste duran 33 tartının üzerine çıktığı zaman ortadaki tartı 60 kilogramı, en alttaki tat 72 kilogramı göstermektedir.En üstteki tartının ağırlığı ortadaki tartının ağırlığının yarısıdır. Buna göre, en üstteki tartı kaç kilogram gösterir? A) 51 B) 52 C) 54 D) 55 E) 58 www.matematikkolay.net     A O Ü O Ü Ü Çözüm: Ege’nin ağırlığı E, Alttaki tartının ağırlığı t Ortadaki tartının ağırlığı t Üstteki tartının ağırlığı t olsun. 72 E t t En alttaki tartı 60 E t Ortadaki tartı Aradaki far      O Ü Ü k t 12 kg dır. En üstteki tartı, ortadakinin yarısı ise 12 t 6 kg dır. 2 O halde; 60 E t 60 E 6 E 54 kg dır. En üstteki tartı sadece Ege’nin ağırlığını göstereceği için 54 kg ‘ı gösterir.           102 Emre bir sinema salonunun A,B,C salonları için bilet satmaktadır. Belli bir sayıda bilet attık tan sonra A salonunda 17, B salonunda 13, C salonunda ise x tane boş koltuk kaldığını görmüştür. Sonra en az kaç bilet satarsam her salondan en az bir bilet satmayı garantilerim diye soru sormuş ve cevabını 38 bulmuştur. Buna göre, x kaçtır? A) 17 B) 18 C) 19 D) 20 E) 21 www.matematikkolay.net Çözüm: A salonunda 17, B salonunda 13, C salonunda x boş koltuk var. 3 salondan da bilet satmayı garantilemek için, en boş 2 salonu doldurmak, sonra da diğer salondan 1 bilet satmalıyız. En boş salonlar A ve B olsaydı; 17 13 1 31 bilet satmak gerekirdi. Ancak 38 miş. O zaman, en boş salonlar A ve C dir. 17 x 1 38 eşitliğini sağlamalıdır. 18 x 38 x 20 buluruz.          169 Banu, üç vagonlu bir yolcu treni için bilet satışı yapmaktadır. Belirli sayıda bilet sattık tan sonra Banu; ilk vagonda 6, ikinci vagonda ise 13 koltuğun boş kaldığını görüyor. Banu; her 3 vagondan da birer bilet satışını garantilemek için en az kaç bilet satması gerek – tiğini hesaplıyor ve sonucu 23 buluyor. Buna göre, trendeki toplam boş koltuk sayısı kaçtır ? A) 24 B) 28 C) 30 D) 33 E) 35 www.matematikkolay.net İlk Çözüm: 3.vagondaki boş koltuk sayısını bilmiyoruz. Her üç vagondan da bilet satışını garantilemek için, En fazla boşluk olan iki vagondaki koltukları bitirip, son vagondan da bir bilet satmak gerekir. 6 vagon İkinci vagon 3. vagon İkinci vagon 13 1 20 oluyor. Demek ki üçüncü vagonda, ilk vagondan daha fazla boşluk vardı. x 13 1 23 x 14 23 x 9 dur. O halde; Toplam boş koltuk sayısı 6 13 9 28 dir.               150