Soru Sor sayfası kullanılarak Üslü Denklem ve Eşitsizlikler konusu altında Nitelikli üslü denklem soruları ile ilgili sitemize gönderilen ve cevaplanan soruları içermektedir. Bu soru tipine ait soruları ve yaptığımız detaylı çözümleri aşağıda inceleyebilirsiniz. Yardımcı olması dileğiyle, iyi çalışmalar…
1.SORU


2.SORU
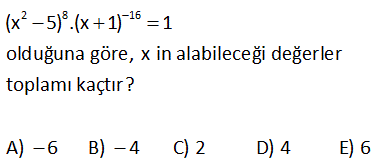
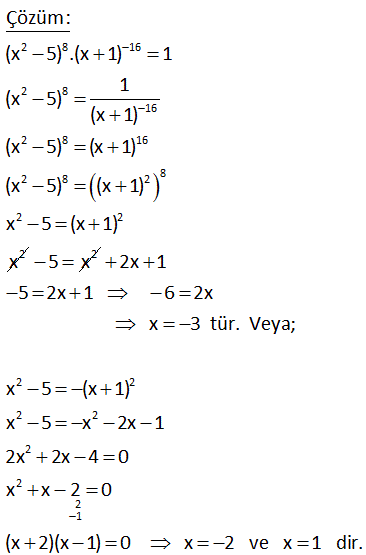
3.SORU


4.SORU


5.SORU


6.SORU
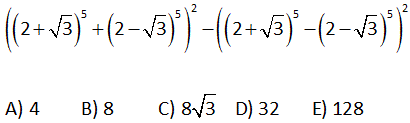

7.SORU


8.SORU
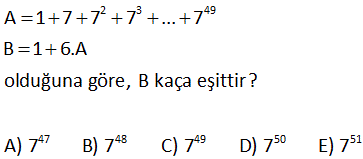

9.SORU
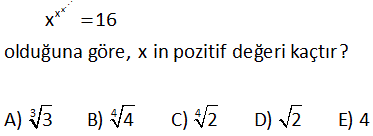

Diğer Soru Tipleri için Tıklayınız.
Konu Anlatımı İçin Tıklayınız.
Abone olarak daha fazla sayıda soru sorabilirsiniz. Abone olmak için Tıklayın.
Not: Bu sayfadaki sorular, ziyaretçilerimiz tarafından gönderilmiştir. Telif hakkını ihlal eden durumlar için lütfen iletişim sayfasından bize bunları bildiriniz. Kısa süre içerisinde sitemizden bu sorular kaldırılacaktır.
Not: Bu sitede yayınlanan çözümler, tamamen bu site için hazırlanmıştır. İzinsiz olarak yayınlanıp, çoğaltılması yasaktır.
3x 4 2x 4 y x ve y tam sayılar olmak üzere, 2 2 2 için x y toplamı kaçtır? A) 21 B) 25 C) 29 D) 31 E) 35 3x 4 2x 4 y 2x 4 x 8 2x 4 y 2x 4 x 8 y x 8 Çift Çift Tek Tek olmalı x 8 0 2x 4 x 8 y 2.8 4 y 20 y 21 Çözüm: 2 2 2 2 2 2 2 (2 1) 2 (2 1 ) Çift olmalı 2 sadece 2 olduğunda tek olur. Bu nedenle x 8 dir. 2 (2 1) 2 2 (1 1) 2 2 .2 2 2 y 2 y 21 buluruz. x y 8 21 29 buluruz.15 2 8 16 (x 5) .(x 1) 1 olduğuna göre, x in alabileceği değerler toplamı kaçtır? A) 6 B) 4 C) 2 D) 4 E) 6 2 8 16 2 8 16 2 8 16 2 8 2 8 2 2 2 Çözüm: (x 5) .(x 1) 1 1 (x 5) (x 1) (x 5) (x 1) (x 5) (x 1) x 5 (x 1) x 2 5x 2 2 2 2 2 2 2 1 2x 1 5 2x 1 6 2x x 3 tür. Veya; x 5 (x 1) x 5 x 2x 1 2x 2x 4 0 x x 2 0 (x 2)(x 1) 0 x 2 ve x 1 dir. x’in değerleri toplamı 3 ( 2) 1 4 buluruz. 50 a 1 2a 4 3a 9 b 4 a ve b birer pozitif tam sayıdır. 5 5 5 3.5 olduğuna göre, a b toplamı kaçtır? A) 3 B) 5 C) 7 D) 8 E) 15 a 1 2a 4 3a 9 b 4 6 6 6 b 4 6 b 4 6 b 4 Çözüm: 5 5 5 3.5 bu eşitliğin sağlanması için eşitliğin sol tarafındaki sayıların üsleri eşit olmalı. a 1 2a 4 a 5 tir. 3a 9 2a 4 a 5 tir. 5 5 5 3.5 3.5 3.5 5 5 b 4 6 b 10 du r. ab51015 bulunur. 52 a b 2x 3 y 7 eşitliği a ve b nin sıfırdan farklı bütün reel sayı değerleri için doğru olduğuna göre, x y nin alabileceği değerler çarpımı kaçtır? A) 44 B) 11 C) 11 D) 22 E) 44 Çözüm: 1’in tüm kuvvetleri 1’dir.0’ın 0’dan farklı bütün kuvvetleri 0’dır. Buna göre ifadelerin içlerini önce 0’a sonra 1’e eşitleyelim. 1.Durum 3 2x 3 0 2x 3 x 2 y 7 0 y 7 3 3 14 11 x y 7 dir. 2 2 2 2.Durum 2x 3 1 2x 4 x 2 y 7 1 y 1 7 y 6 x y 2 6 4 tür. Bu değerlerin çarpımı 11 4 22 bulunur. 2 68 2n 4 n 2 n 2 n 2 olmak üzere 9 a ve a 2 2 olduğuna göre, a hangisi olabilir? 1 2 3 3 A) B) C) D) 1 E) 3 3 4 2 2n 2 2 n 2 2n 4 n 2 n 2 4 4 n 2 n 2 2n 4 2 (n 2) n 2 Çözüm: İki ifadeyi taraf tarafa bölelim. 9 a 2 a 9 9 a 2 4 4 a a 9 a a 4 n2 2 2 9 3 a 4 2 3 a dir. 2 78 5 5 2 5 5 2 2 3 2 3 2 3 2 3 A) 4 B) 8 C) 8 3 D) 32 E) 128 5 5 2 2 2 2 2 2 2 Çözüm: 2 3 a ve 2 3 b olsun. Sorudaki ifade; a b a b olur. a 2ab b a 2ab b a 2 2abb 2 a 2 2ab b 5 5 5 5 5 4ab olur. 4ab 4 2 3 2 3 4 2 3 . 2 3 4. 4 3 04.Oca 04.Oca 4 buluruz. 83 5 5 y x ve y pozitif tam sayılar olmak üzere, 2x 3y 3x y 0 olduğuna göre, x ifadesinin en küçük değeri kaçtır? A) 16 B) 25 C) 32 D) 64 E) 125 5 5 5 5 5 5 2 5 Çözüm: 2x 3y 3x y 0 2x 3y 3x y 2x 3y 3x y 2x 3y 3x y eşitliği sağlanmalıdır. Tek kuvvet alındığından, bunlar birbirine eşit olmalıdır. 2x 3y 3x y 2x 3y 3x y 2x 3x y 3y 5x 2y y 5 En küçük x 2 , y 5 tir. x 2 32 buluruz. 85 2 3 49 47 48 49 50 51 A 1 7 7 7 … 7 B 1 6.A olduğuna göre, B kaça eşittir? A) 7 B) 7 C) 7 D) 7 E) 7 2 3 49 2 3 49 2 3 49 2 3 49 07.Tem 07.Tem 07.Tem 07.Tem 49 50 Çözüm: A 1 7 7 7 … 7 6A 6 6.7 6.7 6.7 … 6.7 olur. 1 eklersek; 6A 1 7 6.7 6.7 6.7 … 6.7 07.Tem 7 buluruz. 80 x x 3 4 4 x 16 olduğuna göre, x in pozitif değeri kaçtır? A) 3 B) 4 C) 2 D) 2 E) 4 x x 16 Çözüm: x 16 verilmiş. Sonsuz sayıda x üzeri x , 16′ ya eşitse; ilk x sayısının üzerinde de aynı şekilde sonsuz sayıda x üzeri x olduğu için buraya direk 16 yazabiliriz. Yani; x 16 olur. Bunu çö 4 4 4 4 4 zelim. x 2 x 2 x 2 buluruz.71

